Fast Multipole

Fast Multipole

L. Greengard, V. Rokhlin: A fast algorithm for particle simulations. J. Comp. Phys., 73, 1987.

C. R. Anderson: An implementation of the Fast Multipole Method without multipoles.. SIAM J. Sci. Stat. Comput. 13(4), 1992.

---

Complexity of Fast Multipole

Lets do a computation with $N = 10^6$ particles assuming that $N$ computations take 1 hour

• $O(N)$ algorithm $\to$ 1 hour
• $O(N\log N)$ algorithm $\to$ $14$ hours
• $O(N^2)$ algorithm $\to$ $10^{6}$ hours, or 114 years

---

Fast Multipole Method:

• define a pseudo particle (as in Barnes-Hut) for each cell $\to$ accumulated mass located in centre of mass
• force computation:
  1. between particles in the same or in adjacent cells: add particle–particle force
  2. between particles in separated cells:
     • add forces between corresponding pseudo-particles;
     • accumulate that force to all particles of a pseudo particle

---

Fast Multipole Method

Image from the Master thesis of Fabio Gratl

---

Required kernels

P2M: Particle to Multipole

• in Barnes-Hut this involved summing the mass, and computing the center of mass

  $\to$ locate centre of mass $X_l := \frac{1}{M_l} \sum_j m^{(l)}_j x^{(l)}_j$

  $\to$ accumulated mass $M_l := \sum_j m^{(l)}_j $

• in FMM: use multipole expansion

---

Constructing Multipoles (M2M/P2M)

2 Approaches:

Original Approach of Greengard/Rohlkin, 1987

• similar concept as Taylor series
• complicated to derive, esp. in 3D (spherical harmonics)
• complicated formula for hierarchical assembly

---

Constructing Multipoles (M2M/P2M)

2 Approaches:

Or: inner/outer ring approximations by Anderson, 1992

• derived via numerical integration of an integral formula
• uniform interaction with child and remote boxes
• hierarchical assembly via evaluation of potentials at integration points

---

Anderson’s method

Fundamental idea: represent potential via a surface integral

\[\Psi_a (\vec{x}) = \int\limits_{S^2} g( a \vec{s} ) \left( \sum\limits_{n=0}^\infty \left( \frac{a}{r} \right)^{n+1} Q_n(\vec{s} \cdot \vec{x}_p ) \right) ds\]

• in spherical coordinates $\vec{x} = ( r, \theta, \psi)$,
• with suitable $Q_n$ (charges or mass)
• $\vec{x}_p = ( 1, \theta, \psi)$,
• $g( a \vec{s} )$ the potential on a sphere of radius $a$ that contains all particles

---

Anderson’s method

• and use numerical integration to compute the integral

\[\Psi_a (\vec{x}) \approx \sum\limits_{i=1}^K w_i \, g( a \vec{s}_i ) \left( \sum_n ( \frac{a}{r} )^{n+1} Q_n(\vec{s}_i \cdot \vec{x}_p ) \right)\]

• using $K$ integration points $\vec{s}_i$ on the sphere $S^2$ (weights $w_i$)
• and choosing $M$ relative to accuracy of integration rule

---

Anderson’s method

\[\Psi_a (\vec{x}) \approx \sum w_i \, g( a \vec{s}_i ) \left( \sum\limits_n \left( \frac{a}{r} \right)^{n+1} Q_n(\vec{s}_i \cdot \vec{x}_p ) \right)\]

---

Required kernels

P2M: Particle to multipole

• Original approach: compute multipole expansion, i.e. “Taylor-series”
• With Anderson’s method: compute surface integral with numerical integration
  • approximate potential caused by all particles of the current box
  • evaluate and accumulate particle potentials at positions $a \vec{s}_i $ to obtain values $g( a \vec{s}_i )$

---

Required kernels

M2M: Multipole to Multipole

---

Upward Pass

### Subdivide domain into quadtree/octree - start in root node - descent into subdomains and subdivide for $L$ levels (can have multiple particles per cell at lowest level) Add levels - Next: 1. P2M: particle to multipole 2. M2M: multipole to multipole

---

Required kernels

M2L: Multipole to Local

• box–box interactions occur at multiple levels

  $\to$ as particles are part of all parent/grand-parent pseudo particles, the interaction between two particles might be captured by box–box interactions on multiple levels

  $\Rightarrow$ make sure that each particle–particle interaction is considered exactly once!

---

Required kernels

M2L: Multipole to Local

• force computation between pseudo particles occurs, if:
  1. pseudo particles are not in cells that are direct neighbours (requires particle–particle interaction, no approximation via pseudo particles allowed)
  2. interaction between the boxes that contain those pseudo particles is not considered on coarser levels

  $\to$ considers comparably few interactions on each level that are ``nearby’’ but neither direct neighbours nor too far away

---

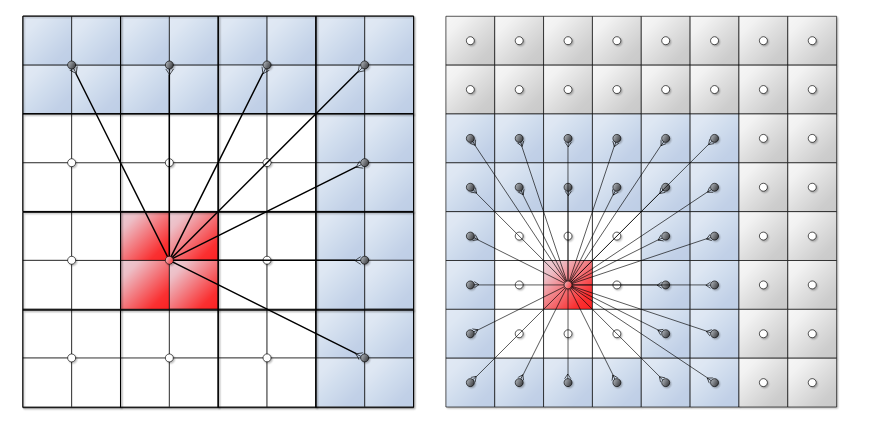
“Horizontal” Pass

</img>

---

“Horizontal” Pass

Compute forces – far-field (M2L)

• For a cell $C_l$:
  • compute interactions with cells that are not direct neighbors and have not been considered on previous levels

Compute forces – near-field (P2P)

• For a cell $C_L$ on the finest level $L$:
  • compute particle to particle forces for neighboring cells and within the cell

---

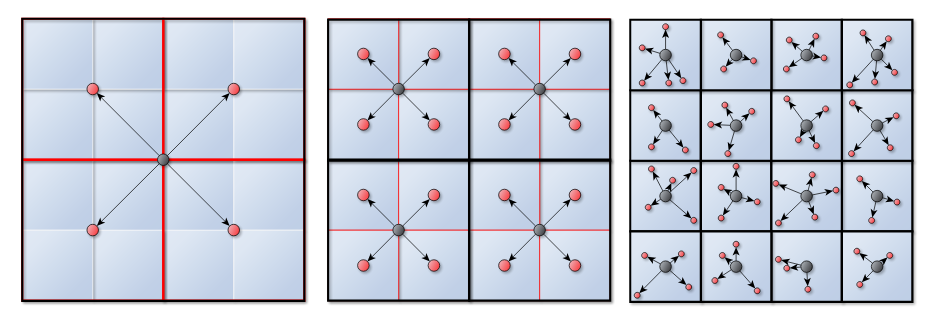
Required kernels: Downward Pass

• For a leaf cell:
  • compute local to particle interaction (L2P)
• For any other cells:
  • compute a local to local interaction (L2L)

---

Required kernels: Downward Pass

</img>

---

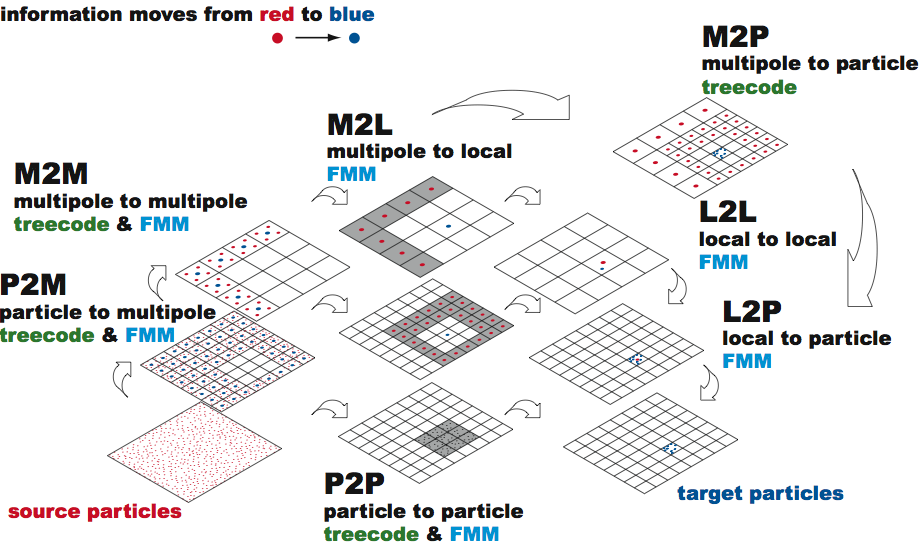
Fast Multipole Method – Summary

R. Yokota:

https://www.bu.edu/pasi/courses/12-steps-to-having-a-fast-multipole-method-on-gpus/

</img>

---

Fast Multipole Method – Summary

1. Initialization: Choose a number of levels such that there are approx. $s$ particles per cell at the finest level. $\to$ $N/s$ cells

2. Upward Pass: Beginning at the finest level create multipole expansions (P2M). Expansions cells at higher levels formed by the merging (M2M).

3. Downward Pass: Compute the far-field (M2L) and near-field (P2P). Convert the multipole expansion into a local expansion about the centers of all cells (L2L/L2P).

---

Fast Multipole Method – Summary

Accuracy:

• depends on accuracy of integration rule

  $\to$ determined by number of integration points

• in practice: can be increased to allow approximations that are accurate up to machine precision

---

Fast Multipole Method – Summary

Complexity:

• computation of box-approximations, i.e., all $g( a \vec{s}_i )$

  $\to$ constant effort per box (leaf and inner boxes)

  $\to$ thus $O(N_\text{B})$ effort ($N_\text{B}$ boxes);

• if max. number of particles per box is constant then $O(N)$ for $N$ particles

• computation of forces

  $\to$ multilevel algorithms leads to $O(N)$ effort

---

Comparison of Barnes-Hut and FMM

Approximate potential of sets/clusters of particles

1. Barnes-Hut
   • pseudo particles in tree cells
   • $\theta$-criterion to determine far-field
2. Fast Multipole
   • higher-order representations necessary!
   • no $\theta$-criterion to tune accuracy (instead choose number of terms in expansion)

---

Comparison of Barnes-Hut and FMM

Hierarchical computation of box potentials

1. Barnes-Hut
   • combine pseudo particles in child cells
2. Fast Multipole
   • generate high order box potentials
   • (accumulate approximate potentials of child boxes to approximate potential of parent box $\to$ needs to be derived for high-order representation)